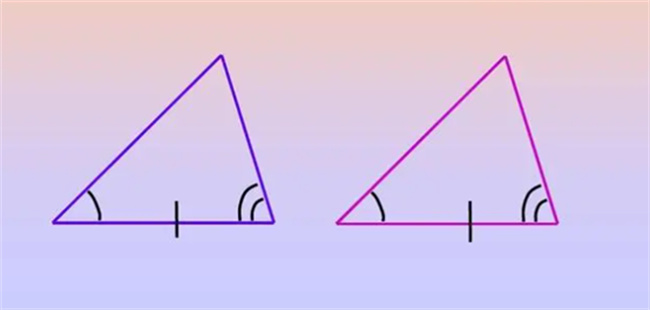
要想有效判断，主要就是按照下面的这些方式。“边边边”、“边角边”、“角边角”、“角角边”、“直角、斜边、边”。在进入到初一的时候就会学习，不过在学习的时候也需要了解，有着不一样的性质。

全等三角形性质

主要的性质就在于全等三角形的对应角相等、对应边相等，重合顶点又被称之为对应顶点，对应边的高是完全相等。对应角的角平分线相等，对应边的中线相等。全等三角形的周长以及面积是相等的，对应角的三角函数数值是相等。

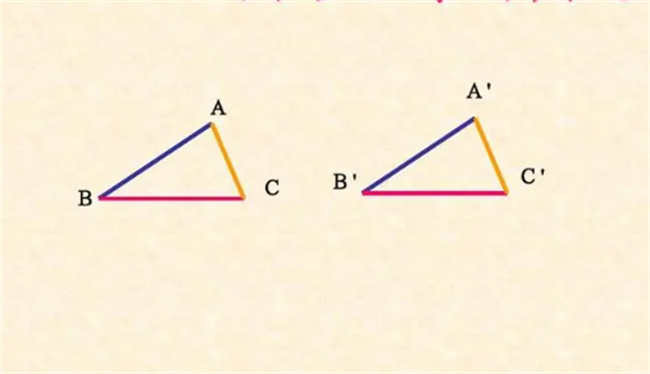
什么是全等三角形？

拥有着许多不一样的性质，其中最为基本的是三条边和三个角是完全一样的。简单来说，两个全等三角形的对应边还有对应角是完全一样的，另外全等三角形还会有一些比较重要的形式。比如两个三角形的三边或者是三个角的度量，分别的相等，那么这个三角形就会被大家称之为全等三角形。

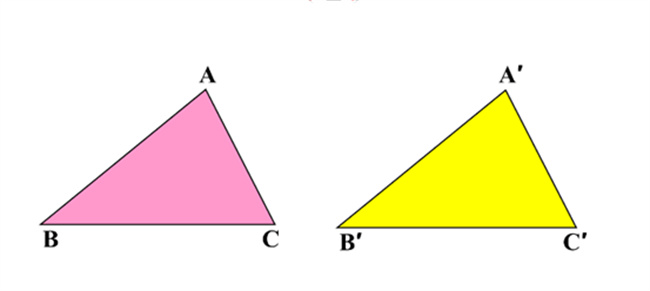
如何证明全等三角形

在证明过程中有很多的细节，比如决定使用SAS法时，需要保证已知的两个角之间边长全部都是共面线段，否则就没有办法构造出全等三角形。如果在使用这一个方法时，还应该注意两个角和边上的边长能不能够确定一个唯一的三角形，如果没有办法确认就没有办法使用这一种方式。在实际的应用还有数学学习中全等三角形是一个重要的概念，是一个基础的概念。掌握性质定理，还有证明的方式，就可以有效解决几何问题，能够帮助大家打下一个坚实的基础。与此同时，对于测量员还有建筑工程师而言，全等三角形本身就是一个理论工具是不可缺少的，在平时使用的过程中都需要使用。